reshu.su

Умножение многочлена на многочлен

§ 13. Тема урока: Произведение многочленов.

Подстановка

Из одного тождества можно получить сколько угодно других тождеств, если всюду в тождестве какую-нибудь переменную заменить одним и тем же выражением.

Пример. В тождестве \( 3x(x-5a)=3x^{2}-15ax \) переменная \( x \) встречается \( 4 \) раза. Заменим всюду эту переменную каким-либо выражением, например \( -7p: \)

\[ \small\tag{\textcolor{#ed5fa6}{1}} 3\cdot(-7p)\cdot (-7p-5a)=\] \[\small 3(-7p)^{2}-15a(-7p). \]

Полученное равенство тоже является тождеством. Для доказательства этого преобразуем отдельно его левую и правую части:

\[\small 3(-7p)\cdot (-7p-5a)= \\ -21p\cdot (-7p-5a)= \\ 147p^{2}+105ap; \] \[\small 3(-7p)^{2}-15a\cdot (-7p)= \\ 3\cdot 49p^{2}+105ap= \\ 147p^{2}+105ap. \]

Следовательно, равенство \( (\textcolor{#ed5fa6}{1}) \) — тождество. Обычно, заменяя какую-либо переменную выражением, говорят, что выполнена подстановка. В нашем примере вместо \( x \) было подставлено выражение \( -7p. \)

Иногда в тождественных преобразованиях и при решении уравнений оказывается полезной замена одинаковых выражений какой-либо переменной.

Пусть, например, нужно доказать тождество:

\[ \small(\textcolor{#3eb489}{2}) \ \ \ (a-2x)^{2}-(a-2x)(a-2x-b)=b(a-2x)\]

Введем подстановку: \( a-2x=y, \) тогда данное равенство \((\textcolor{#3eb489}{2})\) запишется в виде:

\[ \small(\textcolor{#84b2ff}{3}) \ \ \ y^{2}-y(y-b)=by. \]

Преобразуем левую часть равенства:

\[\small y^{2}-y(y-b)=y^{2}-y^{2}+by=by. \]

Мы доказали, что равенство \( (\textcolor{#84b2ff}{3}) \) — тождество, значит, и равенство \( (\textcolor{#3eb489}{2}) \) является тождеством.

Преобразование произведения двух многочленов в многочлен стандартного вида

Пусть дано произведение двух многочленов: \( (a+b)(c+d). \) Попытаемся представить его как многочлен стандартного вида. Обозначим выражение \( a+b \) буквой \( x, \) тогда выражение
\( (a+b)(c+d) \) примет вид \( x(c+d). \) Раскрыв скобки, получим тождество:

\[\small\tag{\textcolor{#ed5fa6}{1}} x(c+d)=xc+xd. \]

Подстановка в тождество \( (\textcolor{#ed5fa6}{1}) \) вместо переменной \( x, \) выражения \( a+b \) приводит к новому тождеству:

\[\small(\textcolor{#3eb489}{2}) \ \ \ (a+b)(c+d)=(a+b)c+(a+b)d \]

Раскрывая скобки в правой части равенства, получаем многочлен, тождественно равный произведению \( (a+b)(c+d): \)

\[\small\small(\textcolor{#84b2ff}{3}) \ \ \ (a+b)(c+d)=ac+bc+ad+bd. \]
Произведение двух многочленов равно сумме произведений каждого члена одного многочлена и каждого члена другого.

Можно полученный результат сформулировать иначе:

Чтобы умножить многочлен на многочлен, достаточно каждый член одного многочлена умножить на каждый член другого.

Мы установили это правило, рассматривая произведение двух двучленов. Можно показать, что правило остается в силе для двух многочленов с любым числом членов в каждом.

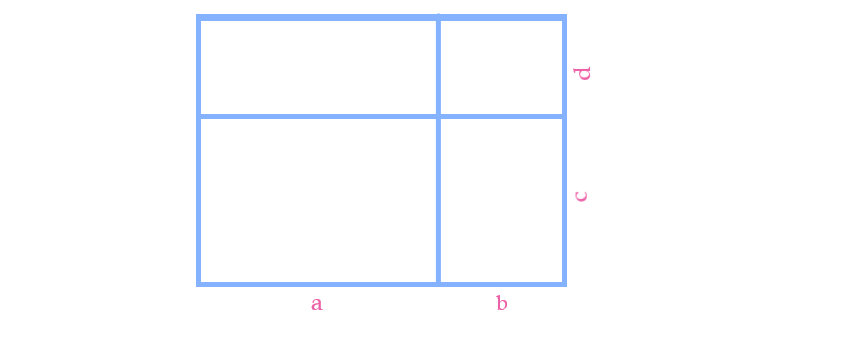
На следующем рисунке дана геометрическая иллюстрация тождества \[\small (a+b)(c+d)=ac+bc+ad+bd. \]

Задачи и примеры решений

№1. Самостоятельно сформулируйте ответы на следующие вопросы:
  1. Как получить сколь угодно много тождеств?
  2. Что такое подстановка?
  3. Как преобразовать произведение двух многочленов в многочлен стандартного вида?

← Следующая тема

\[ \]